更新時(shí)間:2022-11-02 09:33:47 來源:動(dòng)力節(jié)點(diǎn) 瀏覽1663次
二叉樹是一種非常重要的數(shù)據(jù)結(jié)構(gòu),很多其它數(shù)據(jù)結(jié)構(gòu)都是基于二叉樹的基礎(chǔ)演變而來的。對(duì)于二叉樹,有前序、中序以及后序三種遍歷方法。因?yàn)闃涞亩x本身就是遞歸定義,因此采用遞歸的方法去實(shí)現(xiàn)樹的三種遍歷不僅容易理解而且代碼很簡(jiǎn)潔。而對(duì)于樹的遍歷若采用非遞歸的方法,就要采用棧去模擬實(shí)現(xiàn)。在二叉樹遍歷類型中,前序和中序遍歷的非遞歸算法都很容易實(shí)現(xiàn),非遞歸后序遍歷實(shí)現(xiàn)起來相對(duì)來說要難一點(diǎn)。
?三種遍歷方式訪問節(jié)點(diǎn)的順序是一致的,不同之處在于,有的遍歷流程把訪問到的節(jié)點(diǎn)暫存起來,達(dá)成某種條件后再將節(jié)點(diǎn)輸出。
? 前序: 到達(dá)一個(gè)節(jié)點(diǎn)后,即刻輸出該節(jié)點(diǎn)的值,并繼續(xù)遍歷其左右子樹。
? 中序: 到達(dá)一個(gè)節(jié)點(diǎn)后,將其暫存,遍歷完左子樹后,再輸出該節(jié)點(diǎn)的值,然后遍歷右子樹。
? 后序: 到達(dá)一個(gè)節(jié)點(diǎn)后,將其暫存,遍歷完左右子樹后,再輸出該節(jié)點(diǎn)的值。
? 快速確定遍歷序列的方法:
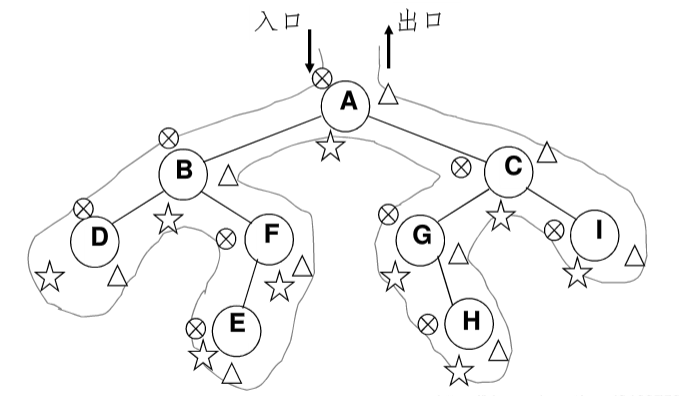
圖中在入口到出口的曲線上用

三種符號(hào)分別標(biāo)記出了先序、中序和后序訪問各結(jié)點(diǎn)的時(shí)刻。
前序遍歷按照 “根結(jié)點(diǎn) - 左孩子 - 右孩子” 的順序進(jìn)行訪問。
遞歸實(shí)現(xiàn)
void preOrder1(BinTree *root) //遞歸前序遍歷
{
if(root!=NULL)
{
cout<<root->data<<"";
preOrder1(root->lchild);
preOrder1(root->rchild);
}
}
非遞歸實(shí)現(xiàn)
根據(jù)前序遍歷訪問的順序,優(yōu)先訪問根結(jié)點(diǎn),然后再分別訪問左孩子和右孩子。即對(duì)于任一結(jié)點(diǎn),其可看做是根結(jié)點(diǎn),因此可以直接訪問,訪問完之后,若其左孩子不為空,按相同規(guī)則訪問它的左子樹;當(dāng)訪問其左子樹時(shí),再訪問它的右子樹。因此其處理過程如下:
對(duì)于任一結(jié)點(diǎn) P:
訪問結(jié)點(diǎn) P,并將結(jié)點(diǎn) P 入棧;
判斷結(jié)點(diǎn) P 的左孩子是否為空,若為空,則取棧頂結(jié)點(diǎn)并進(jìn)行出棧操作,并將棧頂結(jié)點(diǎn)的右孩子置為當(dāng)前的結(jié)點(diǎn) P,循環(huán)至 1); 若不為空,則將 P 的左孩子置為當(dāng)前的結(jié)點(diǎn) P;
直到 P 為 NULL 并且棧為空,則遍歷結(jié)束。
void preOrder2(BinTree *root) //非遞歸前序遍歷
{
stack<BinTree*> s;
BinTree *p=root;
while(p!=NULL || !s.empty())
{
while(p!=NULL)
{
cout<<p->data<<""; //入棧前輸出節(jié)點(diǎn)的值
s.push(p);
p=p->lchild;
}
if(!s.empty())
{
p=s.top();
s.pop();
p=p->rchild;
}
}
}
中序遍歷按照 “左孩子 - 根結(jié)點(diǎn) - 右孩子” 的順序進(jìn)行訪問。
遞歸實(shí)現(xiàn)
void inOrder1(BinTree *root) //遞歸中序遍歷
{
if(root!=NULL)
{
inOrder1(root->lchild);
cout<<root->data<<"";
inOrder1(root->rchild);
}
}
非遞歸實(shí)現(xiàn)
根據(jù)中序遍歷的順序,對(duì)于任一結(jié)點(diǎn),優(yōu)先訪問其左孩子,而左孩子結(jié)點(diǎn)又可以看做一根結(jié)點(diǎn),然后繼續(xù)訪問其左孩子結(jié)點(diǎn),直到遇到左孩子結(jié)點(diǎn)為空的結(jié)點(diǎn)才進(jìn)行訪問,然后按相同的規(guī)則訪問其右子樹。因此其處理過程如下:
對(duì)于任一結(jié)點(diǎn) P,
若其左孩子不為空,則將 P 入棧并將 P 的左孩子置為當(dāng)前的 P,然后對(duì)當(dāng)前結(jié)點(diǎn) P 再進(jìn)行相同的處理;
若其左孩子為空,則取棧頂元素并進(jìn)行出棧操作,訪問該棧頂結(jié)點(diǎn),然后將當(dāng)前的 P 置為棧頂結(jié)點(diǎn)的右孩子;
直到 P 為 NULL 并且棧為空則遍歷結(jié)束
void inOrder2(BinTree *root) //非遞歸中序遍歷
{
stack<BinTree*> s;
BinTree *p=root;
while(p!=NULL||!s.empty())
{
while(p!=NULL)
{
s.push(p);
p=p->lchild;
}
if(!s.empty())
{
p=s.top();
cout<<p->data<<""; //出棧前輸出棧頂節(jié)點(diǎn)的值
s.pop();
p=p->rchild;
}
}
}
后序遍歷按照 “左孩子 - 右孩子 - 根結(jié)點(diǎn)” 的順序進(jìn)行訪問。
遞歸實(shí)現(xiàn)
void postOrder1(BinTree *root) //遞歸后序遍歷
{
if(root!=NULL)
{
postOrder1(root->lchild);
postOrder1(root->rchild);
cout<<root->data<<"";
}
}
非遞歸實(shí)現(xiàn)
后序遍歷的非遞歸實(shí)現(xiàn)是三種遍歷方式中最難的一種。因?yàn)樵诤笮虮闅v中,要保證左孩子和右孩子都已被訪問并且左孩子在右孩子前訪問才能訪問根結(jié)點(diǎn),這就為流程的控制帶來了難題。下面介紹兩種思路。
第一種思路:對(duì)于任一結(jié)點(diǎn) P,將其入棧,然后沿其左子樹一直往下搜索,直到搜索到?jīng)]有左孩子的結(jié)點(diǎn),此時(shí)該結(jié)點(diǎn)出現(xiàn)在棧頂,但是此時(shí)不能將其出棧并訪問,因此其右孩子還未被訪問。所以接下來按照相同的規(guī)則對(duì)其右子樹進(jìn)行相同的處理,當(dāng)訪問完其右孩子時(shí),該結(jié)點(diǎn)又出現(xiàn)在棧頂,此時(shí)可以將其出棧并訪問。這樣就保證了正確的訪問順序。可以看出,在這個(gè)過程中,每個(gè)結(jié)點(diǎn)都兩次出現(xiàn)在棧頂,只有在第二次出現(xiàn)在棧頂時(shí),才能訪問它。因此需要多設(shè)置一個(gè)變量標(biāo)識(shí)該結(jié)點(diǎn)是否是第一次出現(xiàn)在棧頂。
但是這種解法每個(gè)節(jié)點(diǎn)會(huì)入棧和出棧兩次,效率不高。
void postOrder2(BinTree *root) //非遞歸后序遍歷
{
stack<BTNode*> s;
BinTree *p=root;
BTNode *temp;
while(p!=NULL||!s.empty())
{
while(p!=NULL) //沿左子樹一直往下搜索,直至出現(xiàn)沒有左子樹的結(jié)點(diǎn)
{
BTNode *btn=(BTNode *)malloc(sizeof(BTNode));
btn->btnode=p;
btn->isFirst=true;
s.push(btn);
p=p->lchild;
}
if(!s.empty())
{
temp=s.top();
s.pop();
if(temp->isFirst==true) //表示是第一次出現(xiàn)在棧頂
{
temp->isFirst=false;
s.push(temp);
p=temp->btnode->rchild;
}
else //第二次出現(xiàn)在棧頂
{
cout<<temp->btnode->data<<"";
p=NULL;
}
}
}
}
第二種思路:要保證根結(jié)點(diǎn)在左孩子和右孩子訪問之后才能訪問,因此對(duì)于任一結(jié)點(diǎn) P,先將其入棧。如果 P 不存在左孩子和右孩子,則可以直接訪問它;或者 P 存在左孩子或者右孩子,但是其左孩子和右孩子都已被訪問過了,則同樣可以直接訪問該結(jié)點(diǎn)。若非上述兩種情況,則將 P 的右孩子和左孩子依次入棧,這樣就保證了每次取棧頂元素的時(shí)候,左孩子在右孩子前面被訪問,左孩子和右孩子都在根結(jié)點(diǎn)前面被訪問。
void postOrder3(BinTree *root) //非遞歸后序遍歷
{
stack<BinTree*> s;
BinTree *cur; //當(dāng)前結(jié)點(diǎn)
BinTree *pre=NULL; //前一次訪問的結(jié)點(diǎn)
s.push(root);
while(!s.empty())
{
cur=s.top();
if((cur->lchild==NULL&&cur->rchild==NULL)||
(pre!=NULL&&(pre==cur->lchild||pre==cur->rchild)))
{
cout<<cur->data<<""; //如果當(dāng)前結(jié)點(diǎn)沒有孩子結(jié)點(diǎn)或者孩子節(jié)點(diǎn)都已被訪問過
s.pop();
pre=cur;
}
else
{
if(cur->rchild!=NULL)
s.push(cur->rchild);
if(cur->lchild!=NULL)
s.push(cur->lchild);
}
}
}
以上就是關(guān)于“二叉樹的非遞歸遍歷介紹”,如果大家想了解更多相關(guān)知識(shí),可以關(guān)注一下本站的Java在線學(xué)習(xí),相信對(duì)大家一定會(huì)有所幫助的。
 Java實(shí)驗(yàn)班
Java實(shí)驗(yàn)班
0基礎(chǔ) 0學(xué)費(fèi) 15天面授
 Java就業(yè)班
Java就業(yè)班
有基礎(chǔ) 直達(dá)就業(yè)
 Java夜校直播班
Java夜校直播班
業(yè)余時(shí)間 高薪轉(zhuǎn)行
 Java在職加薪班
Java在職加薪班
工作1~3年,加薪神器
 Java架構(gòu)師班
Java架構(gòu)師班
工作3~5年,晉升架構(gòu)
提交申請(qǐng)后,顧問老師會(huì)電話與您溝通安排學(xué)習(xí)