二叉查找樹（Binary Search Tree）又稱二叉排序樹、二叉搜索樹。二叉查找樹是為了實現(xiàn)快速查找而生的，一般情況下，查詢效率比鏈表結(jié)構(gòu)要高。不過，它不僅僅支持快速查找一個數(shù)據(jù)，還支持快速插入、刪除一個數(shù)據(jù)。二叉查找樹要求，在樹中的任意一個節(jié)點都要滿足，其左子樹中每個節(jié)點的值，都要小于這個節(jié)點的值，而右子樹每個節(jié)點的值都大于這個節(jié)點的值。二叉查找樹操作主要分為查找，插入和刪除，下面我們來一一介紹。

1.查找

在二叉查找樹中查找一個節(jié)點，我們先取根節(jié)點，如果它等于我們要查找的數(shù)據(jù)，那就返回。如果要查找的數(shù)據(jù)比根節(jié)點的值小，那就左子樹中遞歸查找；如果要查找的數(shù)據(jù)比根節(jié)點的值大，那就右子樹中遞歸查找。

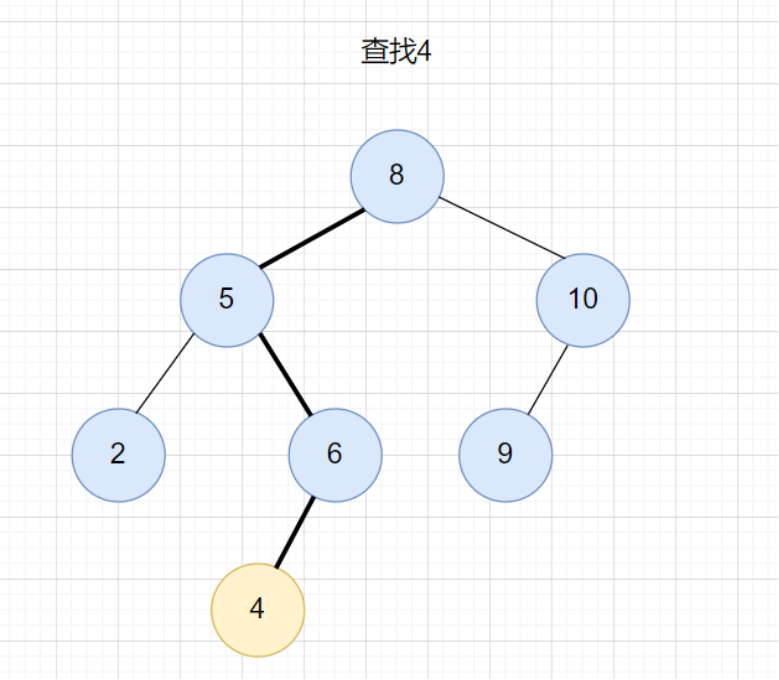
查找的代碼實現(xiàn):

public class BinarySearchTree {
????private Node root;
????public Node find(int data) {
????????Node temp = root;
????????while (temp != null) {
????????????if (data == temp.data) {
????????????????return temp;
????????????} else if(data > temp.data) {
????????????????temp = temp.rchild;
????????????} else {
????????????????temp = temp.lchild;
????????????}
????????}
????????return null;
????}
}

public class Node {
????int data;
????Node lchild;
????Node rchild;
????public Node(int data) {
????????this.data = data;
????}
}

2.插入

插入的操作類似于查找的操作。從根節(jié)點開始，依次比較要插入的數(shù)據(jù)和節(jié)點的關(guān)系。 如果要插入的數(shù)據(jù)比節(jié)點的數(shù)據(jù)大，并且節(jié)點的右子樹為空，就將數(shù)據(jù)直接插入到右子節(jié)點的位置，如果右子樹不為空，那就繼續(xù)遍歷右子樹；如果要插入的數(shù)據(jù)比節(jié)點的數(shù)據(jù)小，并且節(jié)點的左子樹為空，就將數(shù)據(jù)直接插入到左子節(jié)點的位置，如果左子樹不為空，那就繼續(xù)遍歷左子樹。

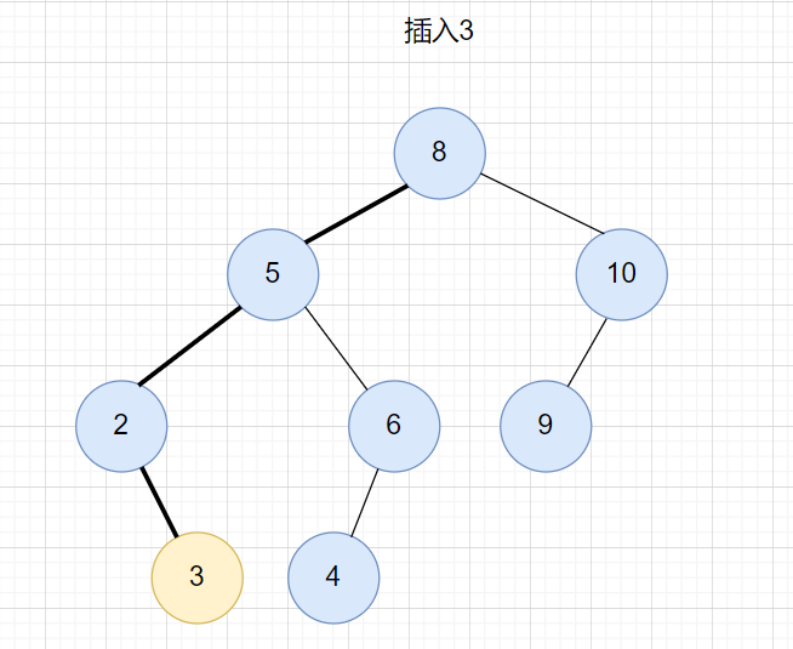
插入的代碼實現(xiàn):

public void insert(int data) {
????????if (root == null) {
????????????root = new Node(data);
????????????return;
????????}
????????
????????Node temp = root;
????????while (true) {
????????????if (data > temp.data) {
????????????????if (temp.rchild == null) {
????????????????????temp.rchild = new Node(data);
????????????????????return;
????????????????}
????????????????temp = temp.rchild;
????????????} else {
????????????????if (temp.lchild == null) {
????????????????????temp.lchild = new Node(data);
????????????????????return;
????????????????}
????????????????temp = temp.lchild;
????????????}
????????}
}

3.刪除

二叉查找樹的查找和插入的操作比較簡單，但是刪除的操作較為復(fù)雜，分為三種情況。 第一種情況，要刪除的節(jié)點是葉子節(jié)點。此時只需要直接將父節(jié)點中指向要刪除節(jié)點的指針置為null即可。如下圖中刪除28。 第二種情況，要刪除的節(jié)點有只有一個子節(jié)點（左子節(jié)點或右子節(jié)點），我們只需要更新父節(jié)點中的指針，讓它指向要刪除節(jié)點的字節(jié)點就可以了。如下圖中的34。 第三種情況，要刪除的節(jié)點有兩個子節(jié)點。這種情況下，我們需要把要刪除節(jié)點的右子樹中最小的節(jié)點替換要刪除節(jié)點。如下圖中的15。

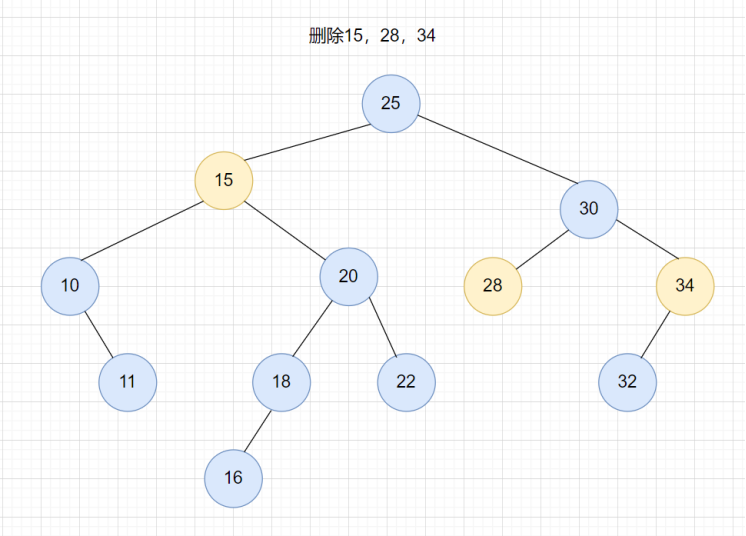
刪除完成后

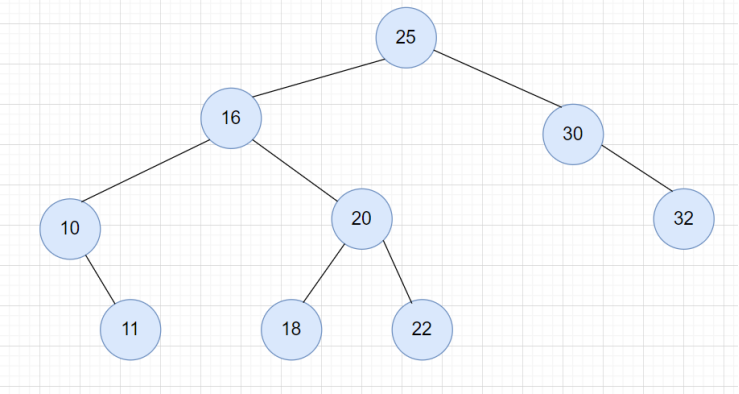
代碼實現(xiàn):

?public void delete(int data) {
????????Node temp = root; ?// temp指向要刪除的節(jié)點
????????Node ftemp = null; // ftemp指向要刪除節(jié)點的父節(jié)點
????????while (temp != null && temp.data != data) {
????????????ftemp = temp;
????????????if (data > temp.data) {
????????????????temp = temp.rchild;
???????????} else {

????????????????temp = temp.lchild;
????????????}
????????}

???????if (temp == null) return; // 沒有找到對應(yīng)的節(jié)點
???????// 若找到，temp就是要刪除的節(jié)點
???????// 要刪除的節(jié)點有兩個子節(jié)點
????????if (temp.lchild != null && temp.rchild != null) {
????????????Node minTemp = temp.rchild; ?// 存儲右子樹的最小節(jié)點
????????????Node fminTemp = temp; // minTemp的父節(jié)點

????????????// 找到右子樹的最小節(jié)點
????????????while (minTemp.lchild != null) {
????????????????fminTemp = minTemp;
????????????????minTemp = minTemp.lchild;
????????????}

????????????temp.data = minTemp.data; // 將最小節(jié)點的值替換到temp中
????????????temp = minTemp; ?// 變成刪除葉子節(jié)點
????????????ftemp = fminTemp;
????????}

????????// 刪除節(jié)點是葉子節(jié)點或者僅有一個節(jié)點
????????Node child; // temp的子節(jié)點
????????if (temp.lchild != null) {
????????????child = temp.lchild;
????????} else if (temp.rchild != null) {
????????????child = temp.rchild;
????????} else {
????????????child = null;
????????}

????????if (ftemp == null) { ?// 刪除的是根節(jié)點
???????????root = child;

????????} else if (ftemp.lchild == temp) {
????????????ftemp.lchild = child;
????????} else {
????????????ftemp.rchild = child;
????????}
????}

以上就是對二叉查找樹操作的相關(guān)介紹，二叉查找樹本質(zhì)上是一棵空樹，或者沒有鍵值相等的結(jié)點，對二叉查找樹的定義也是相對的。想要深入學(xué)習(xí)二叉查找樹的小伙伴可以觀看本站的數(shù)據(jù)結(jié)構(gòu)和算法教程，積累更多關(guān)于二叉查找樹的相關(guān)知識。