更新時間:2021-08-09 16:26:20 來源:動力節點 瀏覽993次
能夠完成以下兩個操作的數據結構叫優先隊列:
可以插入新元素
可以快速取出所有元素的最值。
堆是一顆完全二叉樹。
重要的性質:父節點一定是其所有子孫節點的最值。
一個簡單的堆的示意圖如下:
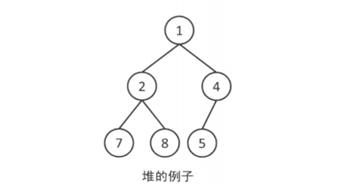
堆的插入:首先在堆的末尾插入該數值,然后不斷向上調整,直到沒有大小顛倒為止
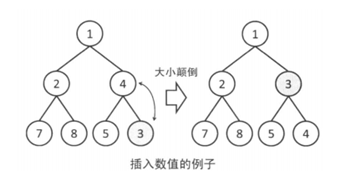
取出最值:最值就在堆頂,即二叉樹的第一個元素。
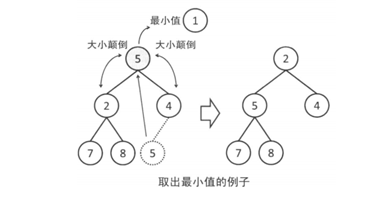
刪除最值:首先將堆的最后一個元素復雜到根節點,并刪除最后一個元素,然后將根節點不斷向下進行調整直到沒有大小顛倒。
時間復雜度:堆的插入和刪除的時間復雜度為O(l o g?n)O(log?n)O(log?n)
注意:刪除和插入具體的向上/下調整的方法,可以看下面的代碼。
優先隊列的實現:我們知道完全二叉是可以通過簡單的數值實現的,如果我們將完全二叉樹中的每個節點進行編號,編號從1開始,編號順序是從上到下從左到右,然后根據這個編號將樹中的節點存儲到數組中,父子關系可以通過下面方式得到:
假設當前節點的編號(數組中的編號)為i ii,則有:
它的父節點的編號為:i/2 i/2i/2(整除)
它的左兒子節點的編號為:2∗i 2*i2∗i
它的右兒子節點的編號為:2∗i+1 2*i+12∗i+1
//最小堆的實現
#include <iostream>
#define Max_N 1005
using namespace std;
int Heap_size;
int Heap[Max_N];
//插入操作
void push(int x)
{
int indx=++Heap_size;//首先插入到最后一個位置
//向上調整
while(indx>1)//只有i>1才會有父節點
{
int parent_indx=indx/2;//父節點編號
if(Heap[parent_indx]<=x)//沒有上下顛倒就結束調整
break;
Heap[indx]=Heap[parent_indx];//大小顛倒就將當前節點上調
indx=parent_indx;
}
Heap[indx]=x;
}
//刪除操作
int pop()
{
int result=Heap[0];//獲取最值
int x=Heap[--Heap_size];//相當于將最后的一個元素放到根節點
int index=1;
while(2*index<=Heap_size)//一定要有子節點
{
int L_son_index=2*index;
int R_son_index=2*index+1;
//比較兒子節點的最值
int Min_index=L_son_index;
if(R_son_index<=Heap_size && Heap[R_son_index]<Heap[Min_index])
Min_index=R_son_index;
//如果沒有上下顛倒就結束
if(Heap[Min_index]>=x)
break;
//上下顛倒就交換
Heap[index]=Heap[Min_index];
index=Min_index;
}
Heap[index]=x;
return result;
}
void Build_Heap(int data[],int n)
{
//創建一個空堆
Heap_size=0;
for(int i=0;i<n;i++)//逐個插入元素
push(data[i]);
}
int main()
{
int n;
int data[Max_N];
cin>>n;
for(int i=0;i<n;i++)
cin>>data[i];
cout<<"使用下面數據構建堆"<<endl;
for(int i=0;i<n;i++)
cout<<data[i]<<" ";
cout<<endl;
Build_Heap(data,n);
cout<<"堆中數據:"<<endl;
for(int i=1;i<=Heap_size;i++)
cout<<Heap[i]<<" ";
cout<<endl;
return 0;
}
/*
9
9 7 10 4 5 19 23 6 7
*/
實際上,大部分情況并不需要自己使用堆來實現優先隊列,我們可以使用C++中,STL里面的priority_queue來實現優先隊列。
以上就是動力節點小編介紹的"優先隊列的詳解",希望對大家有幫助,想了解更多可查看Java教程。動力節點在線學習教程,針對沒有任何Java基礎的讀者學習,讓你從入門到精通,主要介紹了一些Java基礎的核心知識,讓同學們更好更方便的學習和了解Java編程,感興趣的同學可以關注一下。
 Java實驗班
Java實驗班
0基礎 0學費 15天面授
 Java就業班
Java就業班
有基礎 直達就業
 Java夜校直播班
Java夜校直播班
業余時間 高薪轉行
 Java在職加薪班
Java在職加薪班
工作1~3年,加薪神器
 Java架構師班
Java架構師班
工作3~5年,晉升架構
提交申請后,顧問老師會電話與您溝通安排學習